MCHyper is a model checker for HyperLTL (a temporal logic able to express hyperproperties like noninterference) that builds on standard verification techniques from hardware model checking. Thus, it is used to verify a system against a hyperproperty relating multiple system traces. In the following, we introduce you to MCHyper and its interactive online tool interface.

The layout of the tool consists of three main sections: Input, Output and Console. In the Input section, the input of the tool (system, property, options, ...) can be specified. When running the tool with the specified input, the result and some statistics are shown in the Console. The generated files appear in the Output section when the tool finished.

By clicking on the button, the current tab is maximized. Clicking on the button afterwards restores the original layout. Resizing the tabs individually using the sliders in between is also possible. You can try this and the following features directly in the interactive tool instance below.
The current section's content can be downloaded with . For the output section, the content of the currently selected output tab is saved. For the input section, a file is created that contains the whole specification (the content of all tabs and the selected options). Saved specification files can be easily loaded by clicking on and selecting the desired file from the system's file explorer.
To explore predefined examples, one can choose from the drop down list after clicking on .

---

Let's assume we have a reactive system, that let us control a light with an input of zeros and ones. Additionally, we want our system to fulfill a certain property that ensures that the system works as expected.

First, let's focus on the Input section to specify the above mentioned example.

Specifying the system

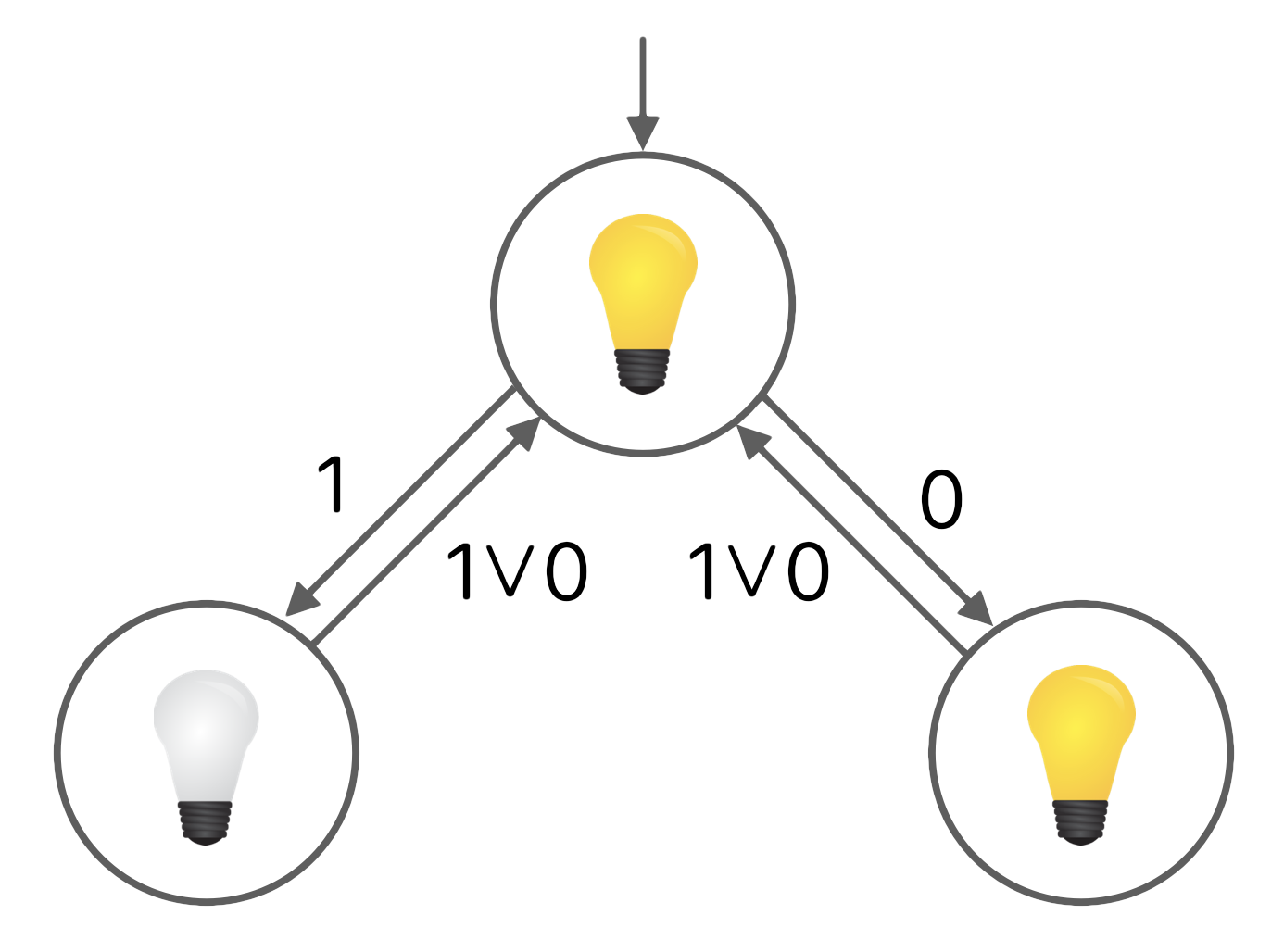
First, we need to have a model of a system that we want to fulfill a property. Let's turn our attention to the following automaton representing our given system.

As specification language, MCHyper supports both Verilog and Aiger (both are hardware description languages to model circuits). To specify the automaton, you can use the System tab in the interface. The language (Verilog or Aiger) is inferred automatically while typing. In Verilog, our automaton can be realized as follows:

Passing the hierarchical path name of the clock identifier (called "clock path") can be done under Options in the Input section. For example, the clock path for the module above is light/clock. The clock path is inferred automatically if the clock identifier is clock, clk or c.

Let's understand why the above Verilog circuit mathes the desired automaton. In our module, we keep track of the current state in the state register. The constant STATE_0 refers to the start state, STATE_1 refers to the right state and STATE_2 to the left. In the register l we remember if the light is currently ON or OFF and assign this value to the output light. On every clock tick, we change the state and the light register depending on the current state and the input given in the in parameter just like the underlaying automaton specifies it.

Since MCHyper only supports Aiger as input, the system specified in Verilog is converted to Aiger before using the tool Yosys (with the flags -p "proc; techmap -map +/dff2ff.v; delete CLOCK_PATH; synth; aigmap; write_aiger -ascii -symbols" where CLOCK_PATH is replaced by the actual clock path) and is then passed to MCHyper. To skip this preprocessing step or use other flags to create the Aiger circuit from the Verilog code, you can directly enter the system in Aiger. For the sake of completeness, this is the generated Aiger code for the above specified system:

Specifying the Property

Now we need to specify the property that should hold for the system: for all possible input streams the light must behave in the same way. To specify the HyperLTL formula that describes the property, we use the Formula tab in the Input section. In our case, we state that for every pair of traces, the light should always behave the same way over the whole trace:

This formula is written in the EAHyper input format. The grammar for the EAHyper format can be found in the Help tab. In case of syntactical errors in the formula, debugging information is shown in the Console.

It is also possible to use the original MCHyper input format to specify the property. To create new inputs, it is recommended to use the EAHyper format since the MCHyper format is more complicated and harder to write and read. Therefore, there is no need to get in touch with the old format. However, the MCHyper format is still supported for already existing examples. To let the tool know, which language is used, you can select either the MCHyper format or the EAHyper format from the dropdown menu under Options.

In the property, we use light_p to access the output parameter light of the system at some point in the trace p. This is possible for all parameters of Verilog modules or Aiger circuits. It is also possible to have a multi-bit parameter in Verilog. Accessing these parameters in the formula is possible on the bit-level.

The process behind

To set some final options, it is important to know what happens behind the scenes when running the tool. To verify a property for a certain system, MCHyper builds a new circuit with two outputs corresponding to the safety and the liveness part of the property. It contains a copy of the system for every quantifier contained in the formula in which the parameters are renamed to ensure uniqueness, e.g. the parameter p in the system copy x is then named p_x. The created circuit serves as input for the tool ABC, which is used by MCHyper as reachability checker. ABC then tries to set the outputs to 1, when it fails, that means either the safety or the liveness part of the formula is violated. The generated circuit is displayed in the Output tab under Generated Aiger when the tool has finished running. Under Generated Dot, the circuit is visualised. To tell ABC which verification method to choose, you can select one under Options (there is property directed reachability, interpolation and bounded model checking). Additionally, you can specify the desired verbosity of the tool output also under Options. The higher the verbosity the more information will be printed to the Console.

You can find the complete example in the interactive tool below:

---

Understanding the tool output

When running the tool with the above explained input, the following is printed to the console: Counterexample found. Safety violation. This means, that the property does not hold for the given system and the tool has found a counterexample proving this. Therefore, the light does not behave in the same way for all possible pairs of traces. The counterexample found by the tool can be inspected in the Output section under Counter Example.

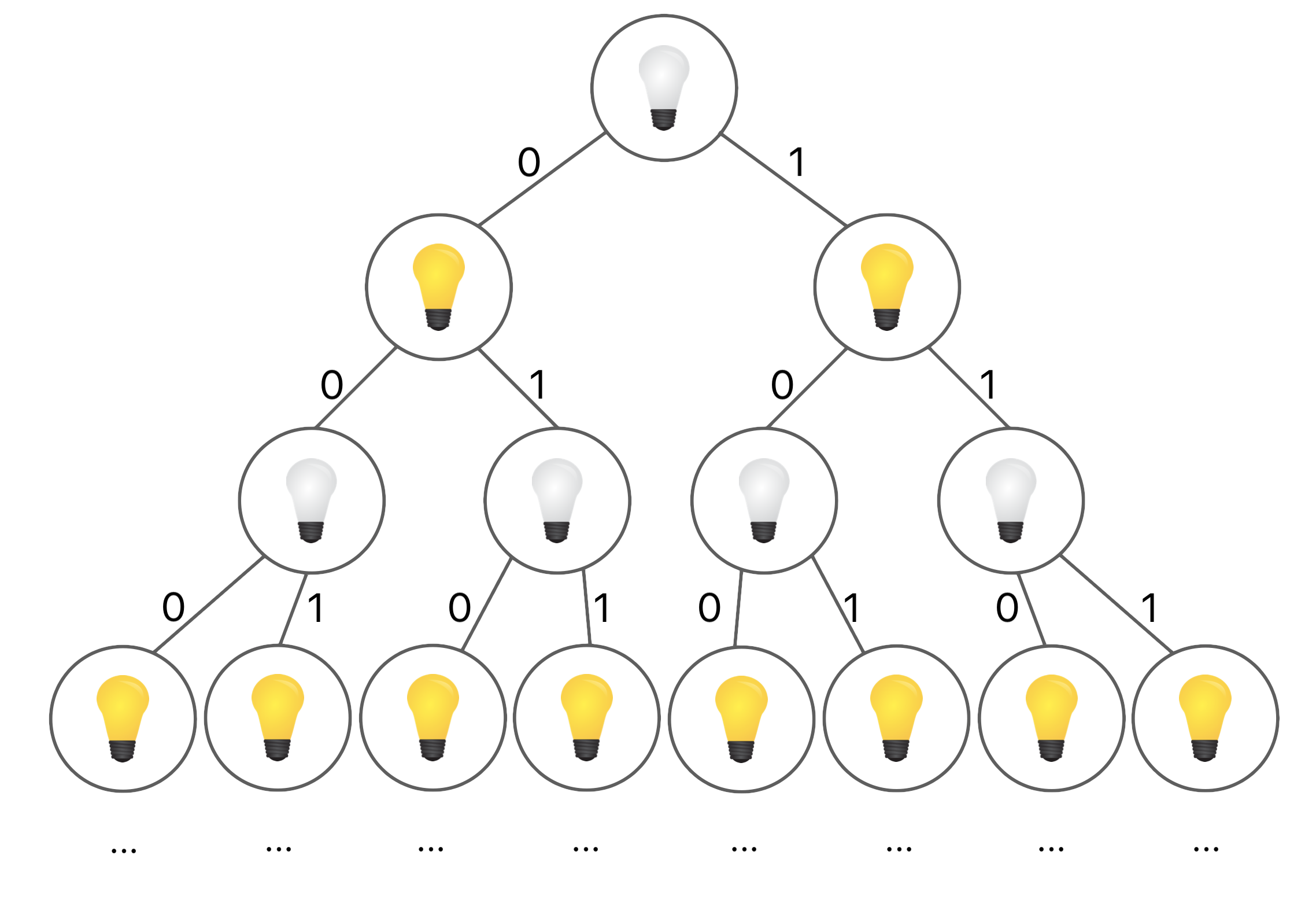
But why does the property not hold? Let's have a look at the possible traces for the given system:

The two red marked traces are different since they differ in the second state. this proves, that not all traces are the same and therefore the light behaves different depending on the input. But we do not have to think about a counter example ourselves. The tool already provided a counter example. So let's have a closer look at it. The counter example gives us an assignment for the parameters in the system. We have already learned that for every quantifier the system is copied once and therefore the parameter in_0 then refers to the parameter in in the system copy 0. The term in_0@0 = 0 then means that this parameter is set to 0 at the time step 0. The counter example states the assignment in_0@0 = 0 and in_1@0 = 1. That means, that we choose the left directory for the first trace and the right directory for the other trace. These decisions then lead to states where the light does not behave the same. Therefore we have already found a violation to our property.

We have seen a system, that does not fulfill the property - you could say that this system contained a bug because it does not match its specification. Instead, a system that has the following traces, would satisfy the property:

We now have to adjust our previous system in order to remove the bug. An automaton that has exactly these traces can look like this:

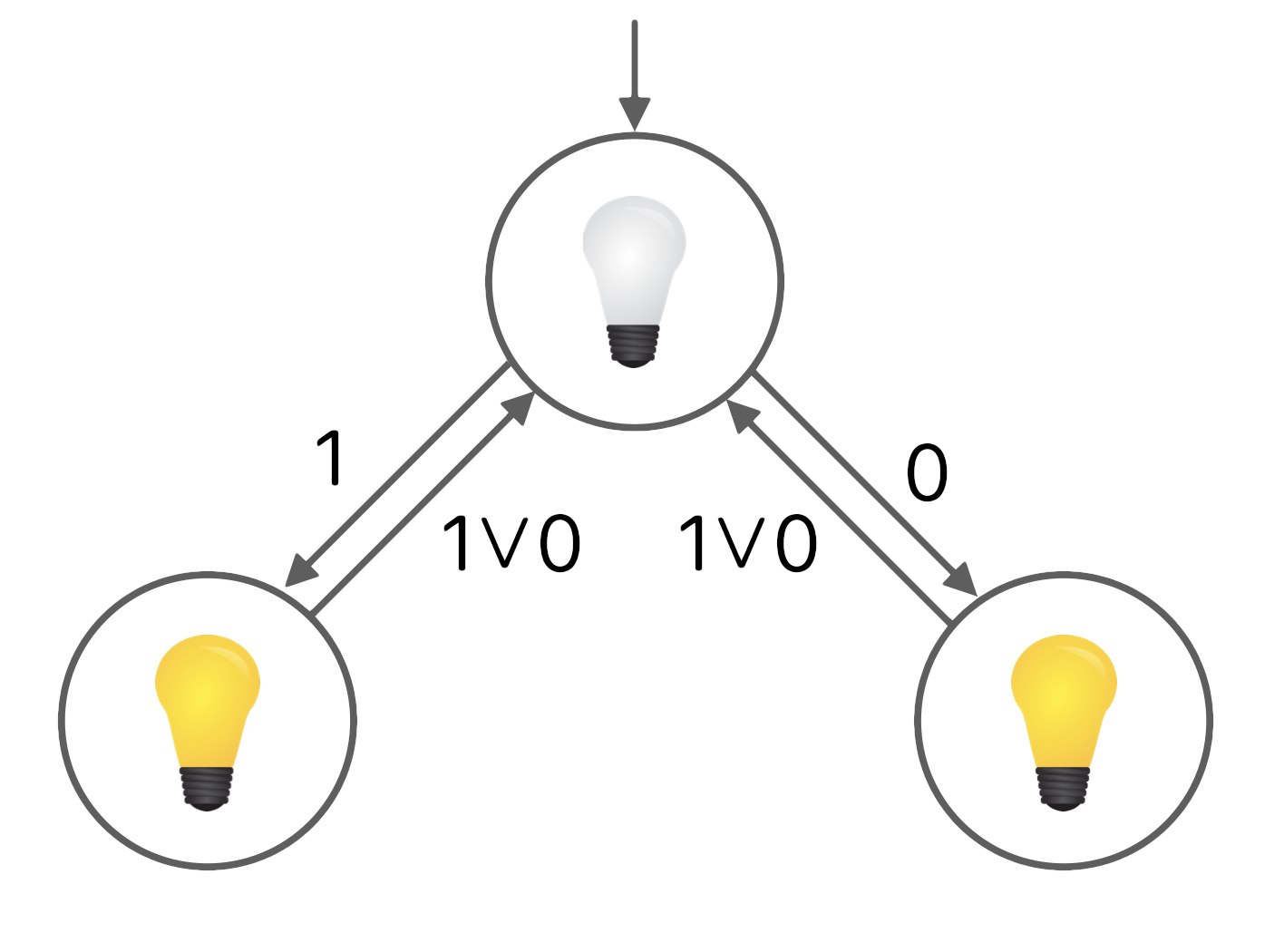
In this automaton, we can already see, that it does not matter which input we provide, the light will always behave the same way. It is worth noting, that the automaton could be simplified and would still accept the same inputs. However, we chose this example because it has a closer relation to the first automaton. A Verilog realization of this automaton is:

The complete working example can be found in the interactive tool below:

---

When running the tool with the corrected example, the tool confirms that the property holds for the system: Property proved. Counter-example is not available. is printed to the Console.

In this example we have a closer look at the exists quantifier and its specialities. Let's use the system from the first example again:

Assuming we want to find out if there exists a trace in this system where the light is always on we can test the system against the property:

After a short inspection, it seems obvious that there is such a trace (for example if the input stream only contains zeros, we always switch between the states, where the light is on). However, if we run the tool with this input, we encounter the message: Counterexample found. The property surely holds for the system, so why is that the case? This is due to the tools implementation.

Therefore the counter example does not prove the exists property wrong but serves as actual prove for the property . The example mentioned above can be experienced in the tool interface below:

---

This means that there can be up to one exists statement nested in a forall statement and vice versa. As example we want to verify in the following system, that for every trace there exists a trace where the light behaves exactly the opposite way.

The property is then formulated as follows:

The property states, that for every trace p there should exist a trace q, that fulfills some condition. Since it would be a way too hard problem to check if there exists such a q for every p we reduce the computational effort needed by defining a strategy. The strategy describes how the parameter assignment for the system copy 1 referring to the existential quantifier must look like depending on the parameter assignment in the system copy 0 referring to the forall quantifier. The strategy can be seen as a function that gets the assignment of the all quantifier and creates an assignment for the existential quantifier. Therefore the forall exists problem is reduced to a forall problem that can be solved. For our example we need to decide, which direction we need to take for trace q when we know which direction was taken in trace p? The answer is simple for that case: We need to choose exactly the opposite input.

How do we realise that in our interface? We specify the strategy in the Strategy tab as another Verilog module. This Verilog module contains all inputs of the system copy 0 as inputs, namely in_0, and all inputs of the system copy 1 as outputs, namely in_1. Then we assign in_1 the negated value of in_0 and we are done.

The strategy in the forall exists case can be seen as "smart black box" playing a simple decision based game. Its target is to always choose the right direction for the trace referring to the existential quantifier as reaction to the direction chosen by the trace referring to the forall quantifier.

The complete example can be experienced in the interface below:

---

For the opposite case, the exists forall alternation, we also define a strategy for trace referring to the existential quantifier. But in this case we do not need to choose the assignment of the existential quantifier in dependeny of the forall quantifier. Instead we just provide an assignment for the existential quantifier. Therefore the Verilog module for the strategy would not contain any input but only outputs.

With the strategy approach mentioned in the last section there is one remaining problem: we are not complete. This means that there are properties that are satisfiable but that we can not prove. This can be the case for properties like forall p. exists q. (light_q <-> X light_p). So why can we not decide about strategies like this one? To do so we need knowledge about the future to define a strategy for the assignment of the existential quantifier since there is an comparison including different time steps.

Fortunately there is a way to fix this: prophecy variables. What is a prophecy variable? We assume that we can guess the value for X light_p and this guess is then stored in a variable v, the prophecy variable. Now we change the formula above to the following: forall p. exists q. (v_p <-> X light_p) -> (light_q <-> X light_p). We need to assign v to some trace and in this case we chose p. In the case that we guess the value for X light_p correctly, we are able to decide the original formula since we then can use v in the strategy for the existential quantifier and do not need to have knowledge about the future.